This post starts with a response to a reader question but leads to a deeper question — do arbitrage-free prices present opportunities to fundamental or directional investors?
One thing I’ll be doing more of is sharing my answers to reader questions. Here’s one that channels a topic that eternally confuses option investors when they learn about skew (emphasis mine):
In your excellent article Lessons from the .50 Delta option, you wrote that by bidding up the put skew, the market makes call spreads more expensive. Combining this with your insights on the deeper understanding of vertical spreads, implied distributions, and thinking of spreads as odds, I was left wondering how the steepness of the skew relates to outright buying or selling options.
Here’s my question: Let’s say the SPX Dec24 call skew (100–105 moneyness) is descending. If I were to buy a call spread with 100/105 moneyness, I’d probably measure it as slightly more expensive than a 100/95 put spread. This aligns with what you’ve been writing. However, what I don’t understand is: if call spreads are more expensive (because the 105 vol is lower than ATMF), wouldn’t it be better to buy 105 calls outright due to the low vol? In my mind, this contradicts the perception we get from the spreads. The market seems to favor upside scenarios and bid up call spreads, yet at the same time, outright calls get cheaper?
Could this have something to do with IVs, deltas, or VRP?
It’s such a great and common question.
My response:
I know it feels like a contradiction. I’ve even framed it that way because it grabs your attention…it really feels like one!
But ultimately it’s not.
Think of option skew creating vertical spread prices that imply a distribution which “corrects” the Brownian motion assumption — namely, that the market is positively skewed but more likely to go down than up.
This is exactly the opposite of empirical results…the market is negatively skewed and a favorite to go up!
The upside call is cheaper because there’s less positive long-tail skew than Black Scholes assumes but the call spread is more expensive because the stock is more likely to go up.
We shift probability to the right but truncate the magnitude of the upside. It’s like betting on a favorite in sports…you’ll probably be right but the upside isn’t as large.
The main point is that the distribution is like a sculpture — the volatility skew moves some clay from the right tail to the left tail, and shifts the whole sculpture rightwards a smidge.
The paywalled Thursday Moontower posts generally dig deeper into investing concepts practically. They’ve been very option-centric lately. However, the most popular one I’ve written recently is not directly about options. It drove 20 paid subs which is an unusually high amount.
[Incidentally, the topic of paywalls, monetization, and so forth is something I’m happy to discuss. In fact, I have a backlog item to come up with a pricing model for “Should I paywall content or not” mostly to itemize most of the major inputs into such a model and their sensitivities or greeks. In any case, the topic of monetization feels under-discussed at least from my aperture. I wonder if that’s because people are hesitant to share. In any case, I see no advantage in being opaque on how to think about monetization. At the end of the day, some amount of what I write is paywalled. A lot of effort goes into but I don’t subscribe to Marx’s Labor Theory of Value — if it’s worth paying for, it’ll get paid for, and if it’s not it won’t.]
Here’s the post, with the paywall removed 🙌
🔎Volatility Depends On The Resolution
Despite the word “volatility” in the title, it’s more germane to the topic of risk broadly than options. It’s not a long post, but it’s a lot to ponder for any investor. The heart of it can be summarized in a line:
Realized volatility depends on sampling frequency
This concept has such a broad appeal and because of my bit above in Money Angle about realized distributions vs theoretical lognormal distributions, it seemed like a good one to unlock.
The substack post is a condensed version of the whole post which includes lots of charts.
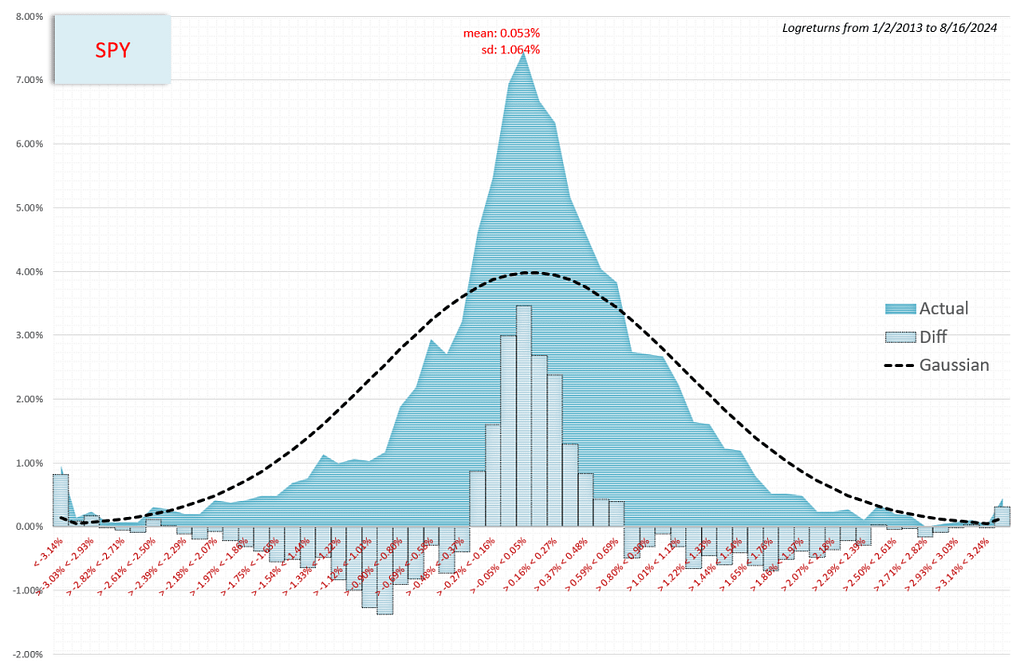
For example, charts that compare realized daily returns vs what is expected theoretically:
The real-world distribution includes:
- Fatter tails (note that greater than 3 st devs is one giant bucket so that’s why even the Gaussian expectation is slopes back up a touch)
- A higher peak (more small moves than theory predicts)
- Positive drift (in theory the drift is approximately [RFR-div yield]/365…a much smaller number than the actual drift has been. Incidentally, people really struggle with the Black-Scholes assumption that a stock has no expected return premium — but that’s actually not the assumption UNLESS you are talking about a specific context — pricing options as a replicating portfolio. Financial Hacking has a great clarification on this.)
The options market adjusts to this empirical reality by:
- Increasing downside put IVs or put skew. This extends the distribution of the left tail but also increases the implied probability of a positive stock return by pushing up the value of ITM calls and therefore call spreads. This shifts the center of the distribution to the right.
- The wing options on both the calls and puts can smirk up increasing the mass in the tails. In price space, this pushes the value of the OTM options relative to the ATM straddle which increases the value of the butterfly (the wings up, relative to the “meat” of the fly). If you think a stock is going to have more small moves than the Gaussian distribution of logreturns predicts then you want to buy a butterfly that’s short the ATM straddle — that is exactly the structure whose value increases.
The volatility skew creates option spread prices that conform to empirical actuarial odds. They “correct” the assumptions baked into the underlying Black-Scholes distribution.
One of the most provocative bunny trails from this conversation is how a long-term call option price that is priced using the RFR for drift will look wildly cheap (and the put expensive) to an investor who assumes higher rates of return because the stock is risky. But if they bid the calls and offered the puts with their return assumptions in the model they would offer risk-less arbitrage profits to option traders would simply do “conversion” strategies.*
If this intrigues you, check out the Warren Buffet section in Real World vs Risk-Neutral Worlds. An option that looks cheap to a fundamental investor focused on the near-term can simultaneously look expensive to an arbitrageur who has no opinion about the underlying but is in the business of squeezing profits from replicating that option for less. Both the directional investor and arbitrage trader can win.
(The loser in a zero-sum paradigm is all the noise traders flipping the stock back and forth in the interim to the delta-rebalancing option trader).
*conversion example
Stock = $100
Interest rate =3%
Theo value of synthetic future (ie long 100 strike call/short 100 strike put) = $103
The call will be worth $3 more than the put. C — P = $3.
Buying the call and selling the put is the same as “buying the 100-strike combo for $3 which is equivalent to buying the synthetic future for $103 — why? Whether you exercise the call in a year or get assigned on the put, you will have paid $100 for the stock. Plus you paid $3 today for that structure, which is why you can say you paid $103 for the stock to be settled in one year.
Imagine a fundamental investor who thinks the stock will be worth $108 in a year (8% RoR instead of RFR) and is willing to pay $5 for the combo ie $105 for a 1-year future on the stock.
They would be buried by arbitrage traders who would sell the combo at $5 and buy the stock for $100 to hedge. At expiry, the arbs will either be assigned on their short call or exercise their long put, guaranteeing they sell the stock at $100. They already bought the stock today for $100 and will have to pay $3 interest to hold it for a year. So at expiry they will deliver the stock to the fundamental investor (selling the stock they bought for $100 at $100…a wash).
The arbitrageur will have paid $3 in interest…but remember they collected $5 in option premium via the combo. Net result: $2 riskless profit
The market hoovers up riskless profits so the arbs will compete to sell the combo to the fundamental investor all the way down to a price of $3 where the combo is fairly priced compared to the RFR.
It doesn’t matter what the fundamental investor or Warren Buffet thinks. If they pay more for the calls relative to the puts than the cost of carry warrants, they get arbed. This has nothing to do with stock distributions, volatility, or any theoretical nerd stuff. A 10-year-old can draw the cash flows on a “conversion” arbitrage.
A “reversal” arbitrage is the opposite…if the combo is too cheap, say $1, you can buy the synthetic future (buy call/sell put), short the stock and at expiration your short stock will be covered by the stock you buy via the future (ie exercise the long call, or get assigned on the put) and the $3 interest you earn on the short stock proceeds covers the $1 premium you paid for the combo leaving $2 of arbitrage profit.
Practically speaking, reversals and conversions, the first arbitrage trades you learn about in options, still have risk.
- There’s pin risk if the stock expires on the strike and you have to guess if you will be assigned on an option or not.
- Interest rates can change from your initial assumption — the overnight interest rates that you pay for long stock or collect as a short rebate change. They can also change dramatically if a stock becomes hard-to-borrow.
- Dividends can be announced, increased, or cut. Higher divs increase put prices relative to calls so if you have a reversal position and a stock announces a dividend your long combo will drop by the dividend
- In other words, a reversal position is long rho and a conversion is short rho (it’s rooting for either interest rates to drop, the stock to become hard-to-borrow, or the stock to pay a larger div)
Comments